Key Exchange Parameters
Shared Secret
Secure Key Exchange
Establish a shared secret over an insecure network, preventing eavesdroppers from knowing the key.
No Prior Secrets
Two parties with no prior knowledge of each other can jointly create a secret key for communication.
Forward Secrecy
Compromise of a long-term key doesn't compromise past session keys, a crucial security feature.
Mathematical Foundation
Based on the difficulty of computing discrete logarithms, a well-studied problem in mathematics.
Visual Learning
Understand the intricate steps of the key exchange with our clear, step-by-step visualization.
Foundation of TLS
Diffie-Hellman is a fundamental component of modern security protocols like TLS, SSH, and IPsec.
About Diffie-Hellman
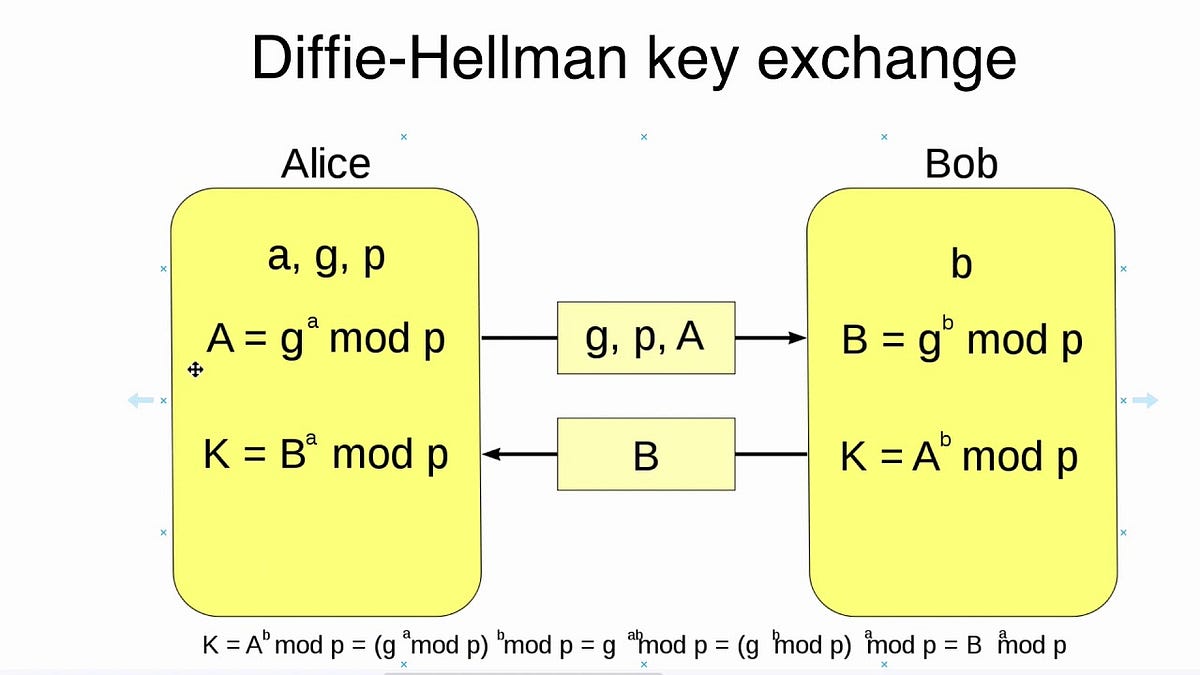
The Diffie-Hellman (DH) Key Exchange is a cryptographic protocol that allows two parties to establish a shared secret over a public, insecure channel. Published in 1976 by Whitfield Diffie and Martin Hellman, it was one of the first practical examples of public-key cryptography.
The core idea is often explained with a paint mixing analogy: Alice and Bob start with a common paint color (public). They each add their own secret color and mix. They exchange their mixed colors publicly. Finally, they each add their original secret color to the mix they received. The result is an identical final color that only they know, as it's computationally infeasible for an eavesdropper to separate the mixed colors.
Mathematically, it uses modular arithmetic and the difficulty of computing discrete logarithms. While the DH method itself is resistant to sniffing attacks, it is vulnerable to Man-in-the-Middle (MitM) attacks if used without authentication (e.g., digital signatures).
How to Use
- Public Parameters: Alice and Bob agree on a public prime number (p) and a generator (g). You can use the defaults or provide your own.
- Private Keys: Alice and Bob each choose a secret private key (a and b).
- Generate & Exchange: Click the "Generate & Exchange Keys" button. The tool will calculate the public keys and then the final shared secret.
- Visualize the Process: The visualization section will show each step of the calculation, from generating public keys to computing the identical shared secret.
- Randomize: Use the "Randomize Parameters" button to try the exchange with different valid numbers.